

The length of the bottom whisker represents how far the lowest value is from the median of the dataset.In the above chart, we can see that the range of salaries is 40,000-10,000 = $30,000. In other words, it tells us if there is a large amount of variation in employee salaries or if they are more or concentrated around the median. The vertical width of the box represents the spread in the data.The line that runs across the middle of the box is the second quartile or the median value of the data.The bottom edge of the box marks the first quartile of the data.The top edge of the box marks the third quartile of the data.This value can help us identify if the dataset is skewed or if there are any potential outliers. The length of the top whisker represents how far the highest value is from the median of the dataset.From the above chart we can see that the highest salary paid by the company is $40,000. The tip of the top whisker (line) marks the maximum value in the data.Let us interpret this chart by looking at its 5 indicators: The image below shows employee salaries of a given company:
Box and whiskers plot excel 2007 how to#
How to Interpret a Box Plotīefore we see how to create a box plot (also called a box and whisker chart), let us first learn to understand and interpret a box plot. In this way, box plots also help us find outliers and can tell if the data is symmetric or skewed.īox plots are especially helpful when you want to compare different sample distributions, and since it provides a 5-point summary of the entire dataset, it is really useful when the datasets you are studying are very large. They can be quite helpful when you want to see how the data is distributed and the range to which the data extends. Why Use a Box Plot?Ī box plot is a great way to visually summarize your data using 5 descriptive indicators. The width of the box basically marks the most concentrated area of the data distribution.Ī box plot can also contain ‘whiskers’ which are simply lines that depict the minimum and maximum values that are outside the first and third quartiles. The main ‘box’ of the box plot is drawn between the first and third quartiles, with an additional line drawn to represent the second quartile, or the ‘median’.
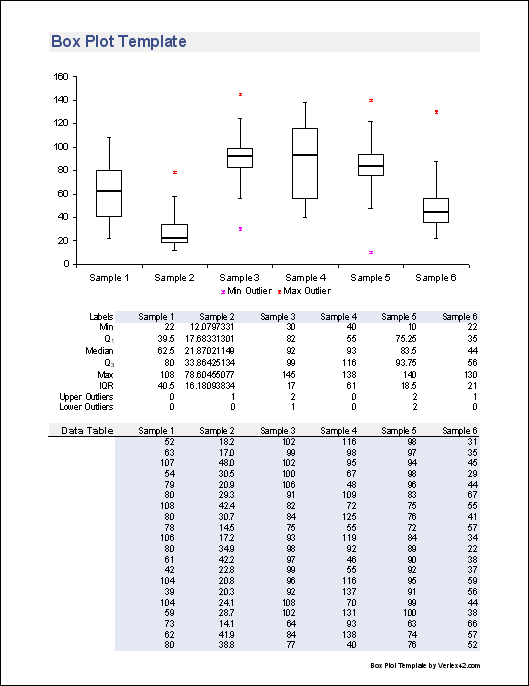
The box plot divides numerical data into ‘quartiles’ or four parts. Again, you can verify this number by using the QUARTILE.EXC function or looking at the box and whisker plot.An example of a Box Plot chart created in Excel This makes sense, the median is the average of the middle two numbers.Ħ. You can verify this number by using the QUARTILE.EXC function or looking at the box and whisker plot.ĥ. In this example, n = 8 (number of data points).Ĥ. This function interpolates between two values to calculate a quartile. For example, select the even number of data points below.Įxplanation: Excel uses the QUARTILE.EXC function to calculate the 1st quartile (Q 1), 2nd quartile (Q 2 or median) and 3rd quartile (Q 3). Most of the time, you can cannot easily determine the 1st quartile and 3rd quartile without performing calculations.ġ. As a result, the whiskers extend to the minimum value (2) and maximum value (34). As a result, the top whisker extends to the largest value (18) within this range.Įxplanation: all data points are between -17.5 and 34.5. Therefore, in this example, 35 is considered an outlier.
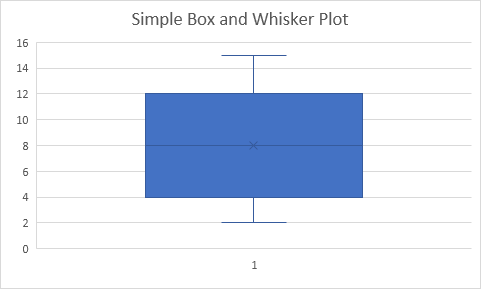
A data point is considered an outlier if it exceeds a distance of 1.5 times the IQR below the 1st quartile (Q 1 - 1.5 * IQR = 2 - 1.5 * 13 = -17.5) or 1.5 times the IQR above the 3rd quartile (Q 3 + 1.5 * IQR = 15 + 1.5 * 13 = 34.5). In this example, IQR = Q 3 - Q 1 = 15 - 2 = 13. Q 3 = 15.Įxplanation: the interquartile range (IQR) is defined as the distance between the 1st quartile and the 3rd quartile. The 3rd quartile (Q 3) is the median of the second half. The 1st quartile (Q 1) is the median of the first half. The median divides the data set into a bottom half. The x in the box represents the mean (also 8 in this example). On the Insert tab, in the Charts group, click the Statistic Chart symbol.Įxplanation: the middle line of the box represents the median or middle number (8).


 0 kommentar(er)
0 kommentar(er)
